Activity links: How to add precedence relations between activities?
When finishing this article, you can take a short "Test Yourself" quiz, to ensure you fully understood this topic.
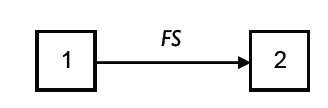
A project network consists of a set of activities, represented as nodes in a network between which links are drawn to represent the technological precedence relations between these project activities. In figure 1, a finish-start precedence relation between activities 1 and 2 is used to imply that activity 2 can not start earlier than the finish of activity 1.
In general, three inputs are required from a project manager to define the precedence relations between activities, as given along the following lines:
- Time-lag of precedence relations: zero or non-zero.
- Type of precedence relation: finish-start, finish-finish, start-start and start-finish.
- Time-lag requirement of a precedence relation: minimal or maximal.
Time-lag
Each precedence relation has a time-lag to denote a minimal time-span between the two activities. Time-lags can be positive, zero or negative, as shown in figure 2.
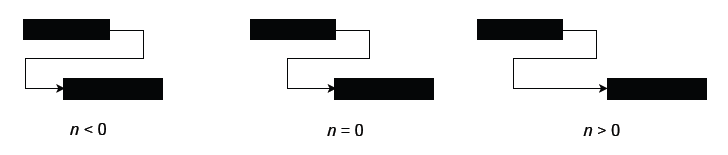
A finish-start relation with a zero time-lag is used to imply that activity 2 can only start after the finishing of activity 1. A zero time-lag implies that the second activity can start immediately after the finishing of the first activity, or later. It does not force the immediate start after the finish of the first activity, but only describes the technological requirements and limitations that exist between two activities.
Similarly, a finish-start relation with a non-zero time-lag n ≠ 0 can be used to imply that activity 2 can only start n time periods after the finishing of activity 1, with n denoting a positive or negative number.
Types of activity link
While the default type of precedence relation between activities is a FS (finish-start) type, there are four different types of precedence relations between two activities, as graphically displayed in the figure below.
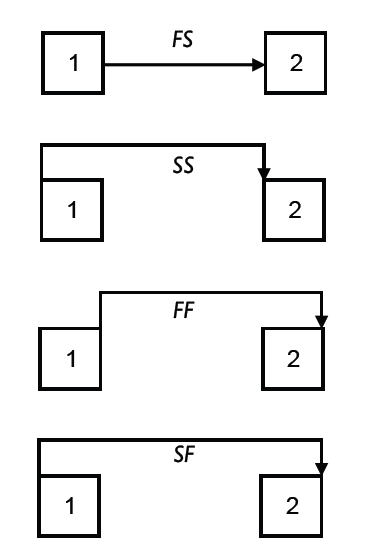
The four types of precedence relations of figure 3 can be summarized as follows:
- FS = n: Activity 2 can only start n time periods after the finishing of activity 1
- SS = n: Activity 2 can only start n time periods after the start of activity 1
- FF = n: Activity 2 can only finish n time periods after the finishing of activity 1
- SF = n: Activity 2 can only finish n time periods after the start of activity 1
with n the time-lag between activities 1 and 2.
Minimal/maximal
While it is assumed that precedence relations imply minimal requirements between two activities, they can be easily extended to maximal requirements. Although most commercial software tools do not incorporate the possibility of maximal time-lags, they are briefly discussed here.
A finish-start relation with a minimal time-lag of n can be used to imply that activity 2 can only start n or more time periods after the finishing of activity 1.
A finish-start relation with a maximal time-lag of n can be used to imply that activity 2 can only start n or less time periods after the finishing of activity 1.
Logically, the extension from a minimal to a maximal time-lag also holds for start-start, finish-finish and start-finish precedence relations. However, they often lead to an increased complexity of the project network. Minimal and maximal precedence relations can, and often will be used in combination.
© OR-AS. PM Knowledge Center is made by OR-AS bvba | Contact us at info@or-as.be | Visit us at www.or-as.be | Follow us at @ORASTalks


