What is my scheduling objective? Minimizing the project lead time
Resource-constrained project scheduling involves the construction of an activity timetable, i.e. the determination of a start and finish time for each project activity, respecting the precedence relations and the limited availability of the renewable resources, while optimizing a predefined scheduling objective (see “Resource constrained project scheduling: What is my scheduling objective?”). In this article, the scheduling objective is assumed to be the minimization of the total duration (or lead time) of the project, which often is a standard scheduling objective option in commercial software tools.
Figure 1 displays a project network with 11 activities and finish-start precedence relations between them. Each number above the node denotes the estimated duration of the activity while the number below the node is used to refer to the resource demand. It is assumed that the availability of the resource is restricted to six units for all periods of the project. The right part of the picture displays an earliest start schedule respecting the precedence relations of the project. Each activity is represented by a rectangle with the horizontal length the activity duration and the vertical height the renewable resource requirement/demand. The earliest start schedule shows a resource conflict between period 8 and 13 since the total use of the renewable resource by activities 3, 4, 5, 6 and 7 exceeds its limited availability of 6. In order to solve this resource conflict, activities need to be shifted further in time to time periods where resources are still available (see “Linking resources to activities: Resource availability and resource demand”).

Figure 1: Project network with activity data and the resource profile of the earliest start schedule
Scheduling objective: minimize the time
Solving resource conflicts results in activity shifts in time in order to schedule them at periods where resources are still available. Activities 3 and 6 cause a resource conflict in figure 1, and must therefore be shifted such that the over-allocations disappear. A simple shift of these activities results in a resource-feasible project schedule as shown in figure 2 with a total project duration of 26.
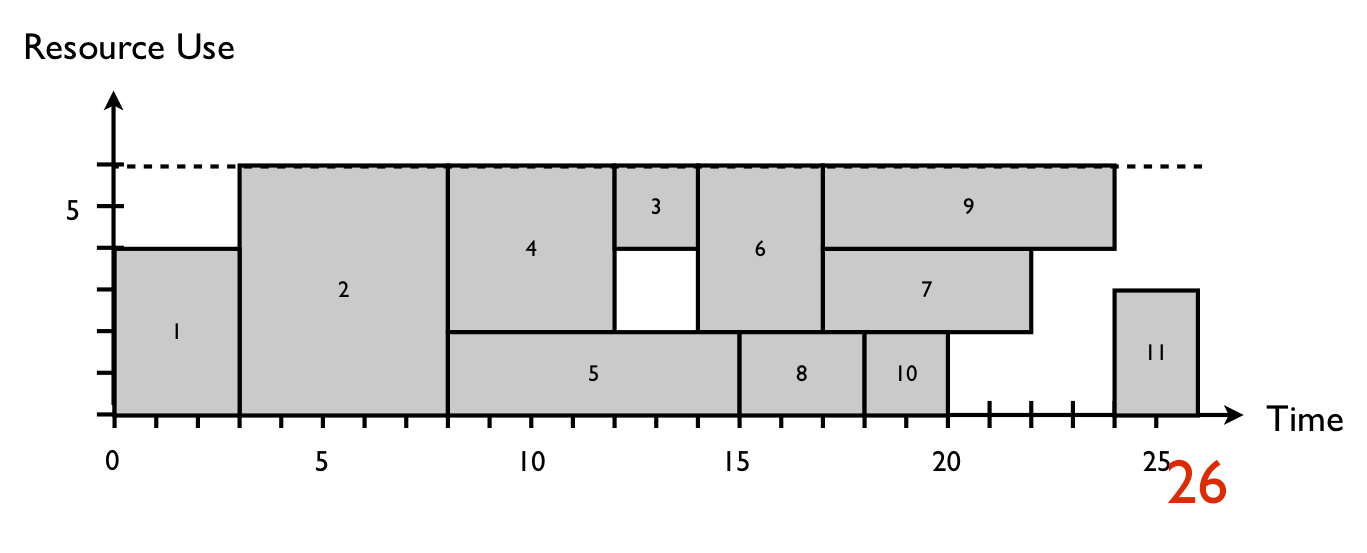
Figure 2: A resource-feasible project schedule obtained by delaying activities 3 and 6
However, this schedule has been constructed without any scheduling objective to optimize, and hence, the shifts of activities 3 and 6 are rather random choices. In figure 3, activities 5 and 6 have been delayed, resulting in a different resource-feasible schedule. In this schedule, time is indeed optimized, resulting in a resource-feasible project schedule with the lowest possible project duration.

Figure 3: A resource-feasible project schedule with the lowest possible total project duration
Note that the critical path in figure 1 is equal to the activity sequence 1 - 2 - 3 - 6 - 9 - 11 while the critical chain of figure 3 is equal to activity sequence 1 - 2 - 4 - 6 - 9 - 11 (see “The critical path or the critical chain? The difference caused by resources”).
© OR-AS. PM Knowledge Center is made by OR-AS bvba | Contact us at info@or-as.be | Visit us at www.or-as.be | Follow us at @ORASTalks


